MathsTips.com

Maths Help, Free Tutorials And Useful Mathematics Resources

Home » Geometry » Understanding Triangle and its Types

Understanding Triangle and its Types

Triangle is a geometrical plane figure. The shape of triangle looks like the figure below:

shape-triangle

A triangle has three sides and three angles. It is a closed figure with three line segments as its boundary. These line segments are called sides. It has three corners called vertices. The symbol for a triangle is Δ

The three vertices are generally named by three consecutive alphabets such as A, B and C or X, Y and Z. A triangle with vertices A, B, and C is denoted by ΔABC.

ABC

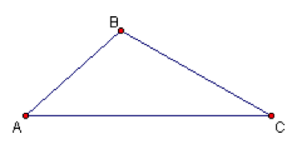
Tri means three and so a Triangle has three angles. These angles are formed by two sides at each of the corners. The angle formed at the vertex A by the two sides AB and AC is called

The three sides and three angles of a triangle together are called the six parts or elements of the triangle.

Now look at the diagram below

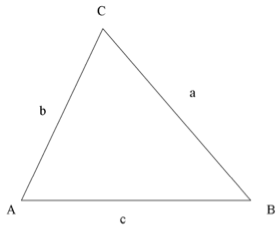
triangle2

The side BC is opposite to vertex A and is also denoted in short by “a”. The sides opposite to B and C are written as b and c. Thus sides BC= a, AC= b and AB= c

Properties of a triangle

  1. The sum of the three angles of any triangle is always 180 degree. <A+ <B + <C =180°
  2. Any angle of a triangle is always greater than zero and less than 180°
  3. Not more than one angle can be 90° or more.
  4. The sum of length of any two sides will always be greater than the length of the third side.
  5. It is a closed plain figure.

Types of Triangles

A triangle can be classified by either its sides: or its angle.

(A) A triangle is classified in three types as scalene, isosceles, or equilateral triangle based on its sides.

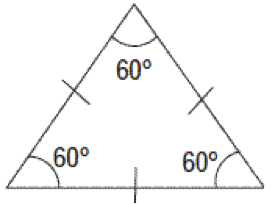
1. Equilateral triangle

A triangle having all sides equal is called an equilateral triangle. It’s all angles are also equal. As sum of three angles of a triangle is 180°, so each angle of an equilateral triangle is 60°.

equilateral-triangle

2. Isosceles triangle

A triangle having two sides equal is called an isosceles triangle. The angles opposite to equal sides are also equal.

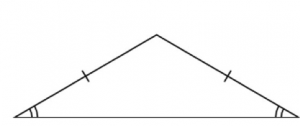
isosceles-triangle

3. Scalene triangle

A triangle having all sides of different length is called scalene triangle.

scalene-triangle

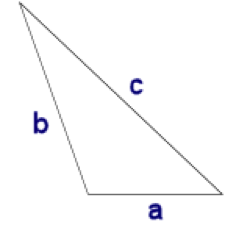
In the figure above, the sides a≠ b≠ c . Hence this is a scalene triangle.

(B) A triangle is classified in three types as acute, right, or obtuse triangle based on its angles:

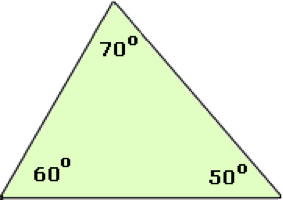
1. Acute triangle

A triangle having all angles less than 90° is called acute triangle.

acute-triangle

In the above triangle, the three angles are 50°, 60° and 70°. All three are less than 90°. Hence it is an acute triangle.

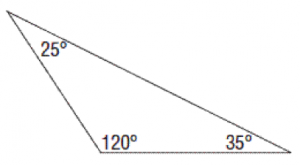
2. Obtuse triangle

A triangle having one angle more than 90° is called an obtuse triangle.

obtuse-triangle

In the triangle above, the three angles are 25°, 35° and 120°.  One of angle is more than 90°. Hence it is an obtuse triangle.

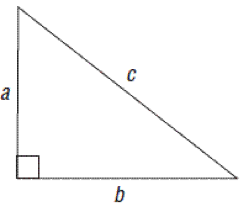
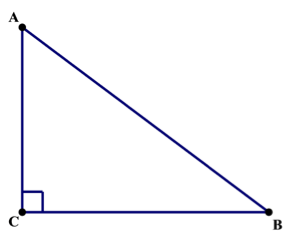
3. Right triangle

If anyone angle of a triangle is 90° , the triangle is called right triangle. The triangle below is a right angle triangle as <ACB is right angle (90°). As sum of three angles of a triangle is 180°,  in a right triangle sum of the other two angles will be 90°.

right-triangle

The side opposite to the right angle is called the hypotenuse.  The hypotenuse is larger than the other two sides. In diagram above, the AB is the hypotenuse and is opposite to the right angle <ACB.

The right triangle has a special property- known as the Pythagorean theorem. The square of length of hypotenuse is equal to the sum of the squares of the lengths of the other two sides. (AC)^{2} + (CB)^{2} = (AB)^{2}.  The Pythagorean theorem is named after the Greek mathematician Pythagoras, who proved this relationship during  570-495 BC. The theorem has a wide range of uses in higher mathematics.

Points to remember about triangles

  1. A triangle has three sides and three angles
  2. A triangle is a plane figure closed by three line segments.
  3. A triangle has three corners called vertices.
  4. The sum of the three angles of a triangle is always 180 degree.
  5. The sum of length of any two sides is always greater than the length of the third side.
  6. A triangle can be classified by either its sides: or its angle.
  7. A triangle is classified as scalene, isosceles, or equilateral triangle based on its sides.
  8. A triangle is classified as acute, right, or obtuse triangle based on measurement of its angles
  9. A triangle with all sides equal is called an equilateral triangle.
  10. A triangle with two sides equal is called an isosceles triangle.
  11. A triangle with all sides of different length is called scalene triangle.
  12. A triangle with a right angle (90°) is called right triangle.
  13. A triangle with all angles less than 90° is called acute triangle.
  14. A triangle having one angle more than 90° is called an obtuse triangle.
  15. Pythagorean Theorem states that the square of length of hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

Questions and Answers

Question 1:

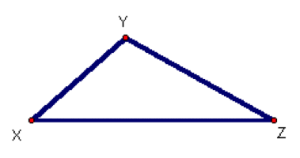
triangleq1

  1. Name the above triangle
  2. How many vertices (corners) the triangle has? Name them
  3. How many sides the triangle has? Name them
  4. How many angles the triangle has? Name them

Solution:

  1. The triangle is ΔXYZ
  2. The triangle has three vertices X, Y and Z
  3. The triangle has three sides XY, XZ and YZ
  4. The triangle has three angles  <X, <Y and <Z

Question 2 : What are the elements (parts) of ΔPQR?

Solution: ΔPQR has three sides and three angles. The three sides are PQ, QR and PR and the three angles are <P, <Q and < R.

Question 3: The two angles of a triangle are 60° and 45°. What is the measurement of third angle?

Solution: Let <A = 60° and <B =45° . Then  <C = ?

The sum of the three angles of any triangle is always 180 degree.

<A+ <B + <C =180°

<C =180° – <A- <B = 180-60-45 = 75°

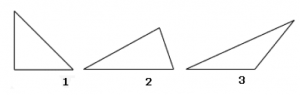
Question 4 : Below are three triangles. Classify them into an acute triangle, obtuse angle and right angle?

triangleq4

Solution:

  1. One angle of Triangle 1 is a right angle (90°) . So Triangle 1 is a right triangle.
  2. All angles of Triangle 2 are less than 90°. So Triangle 2 is an acute angle.
  3. One angle in Triangle 3 is more than 90°. So the Triangle 3 is an obtuse triangle.

Question 5: What is the Pythagorean Theorem?

Solution:

The Pythagorean Theorem states that the square of length of hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides. (AC)^{2} + (CB)^{2} = (AB)^{2} . This can be written also as a^{2} + b^{2} = c^{2}

triangleq5

Exercise

1. How many parts a triangle has?

  1. 3
  2. 6
  3. 7

2. If two angles of a triangle are 30° and 45°, what is measurement of third angle?

  1. 60°
  2. 90°
  3. 105°

3. If each angle of a triangle is equal to 60°, identify the triangle.

  1. Right triangle
  2. Equilateral triangle
  3. Isosceles triangle

4 . If an angle of a triangle is equal to 120°, identify the triangle.

  1. Obtuse triangle
  2. Acute triangle
  3. Right triangle

True or false

6. If an angle of a right triangle is 45°, it will also be an equilateral triangle

  1. True
  2. False

7. A triangle can have more than one right angle

  1. True
  2. False

7. An isosceles triangle can be right triangle also

  1. True
  2. False

Fill in the blank

8. A/An  ………………….. triangle has two sides equal

  1. Right triangle
  2. Obtuse triangle
  3. Isosceles triangle

9. A triangle can not have more than ……….. obtuse angle

  1. 0
  2. 1
  3. 2

10. Which of the following statements is NOT true for a right triangle?

  1. The length of hypotenuse is equal to the sum of the lengths of the other two sides
  2. The length of hypotenuse is equal to the sum of the squares of the lengths of the other two sides
  3. The square of length of hypotenuse is equal to the sum of the squares of the lengths of the other two sides


Comments

Leave a Reply

Your email address will not be published. Required fields are marked *